Since the empty set has no members, when it is considered as a subset of any ordered set, then every member of that set will be an upper bound and lower bound for the empty set. For example, when considered as a subset of the real numbers, with its usual ordering, represented by the real number line, every real number is both an upper and lower bound for the empty set. When considered as a subset of the extended reals formed by adding two “numbers” or “points” to the real numbers, namely negative infinity, which is defined to be less than every other extended real number, and positive infinity, which is defined to be greater than every other extended real number, then: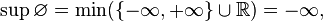 and
and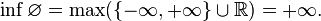
That is, the least upper bound (sup or supremum) of the empty set is negative infinity, while the greatest lower bound (inf or infimum) is positive infinity. By analogy with the above, in the domain of the extended reals, negative infinity is the identity element for the maximum and supremum operators, while positive infinity is the identity element for minimum and infimum.

no comment
som i
no comment
som i
jeg ved slet ikke hvad jeg skal sige
men har alligevel lige lyst til at være tilstede herinde …